Средние величины арифметическая гармоническая Мода Медиана
Средние величины в статистике: сущность, свойства, виды. Примеры решения задач
Наиболее распространенной формой статистических показателей, используемой в экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.
Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности, ведь значения признака отдельных единиц совокупности колеблются в ту или иную сторону под влиянием множества факторов, среди которых могут быть и случайные.
Приведем примеры экономических показателей, основанных на вычислении средней величины и раскрывающих ее сущность:
- расчет средней заработной платы работников предприятия осуществляется делением общего фонда заработной платы на число работников;
- средний размер вклада в банке находят делением суммы вкладов в денежном выражении на количество вкладов;
- для определения средней дневной выработки одного работника необходимо объем работ (количество деталей), выполненных работником за определенный период разделить на число дней в этом периоде.
Мода и медиана
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
Посмотреть решение задачи на нахождение моды и медианы Вы можете здесь
В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:
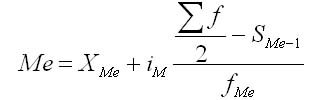
где Хm — нижняя граница медианного интервала;
im — медианный интервал;
Sme— сумма наблюдений, которая была накоплена до начала медианного интервала;
fme — число наблюдений в медианном интервале.
Свойства медианы
- Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее.
- Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения.
- Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины
Графическое определение медианы
Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.
Определение моды в статистике
Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения.
Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда.
Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:
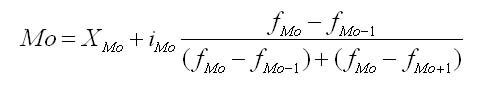
где ХМо — нижняя граница модального интервала;
imo — модальный интервал;
fм0, fм0-1,, fм0+1 — частоты в модальном, предыдущем и следующем за модальным интервалах.
Модальный интервал определяется по наибольшей частоте.
Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д.
Соотношения между средней арифметической, медианой и модой
Для одномодального симметричного ряда распределения средняя арифметическая, медиана и мода совпадают. Для асимметричных распределений они не совпадают.
К. Пирсон на основе выравнивания различных типов кривых определил, что для умеренно асимметричных распределений справедливы такие приближенные соотношения между средней арифметической, медианой и модой:
Медиана [ править | править код ]
У одномерного распределения медиана — квантиль уровня 0,5. Иными словами, медиана — это такое число m 
Преимущества: Медиана согласуется с интуитивным пониманием «среднего». К тому же, даже очень «дикие» выбросы изменяют медиану незначительно. Например, если к сотне бедняков (доходы равномерно распределены от 0 до 1 $) добавить одного миллиардера (1 млрд $), среднее сместится от 0,5 $ до 10 млн $, в то время как медиана — от 0,5 $ до 0,505. Монотонная функция не изменяет медиану — для любой монотонной f ( x ) 

Недостатки: плохо работает для многомерных распределений со сложной взаимосвязью компонентов. Сложна в расчёте.
Структурные средние величины. Мода и медиана
Похожие вопросы
- Теория статистики — Структурныесредниевеличины. Модаимедиана
Модаимедиана. Для характеристики структуры статистической совокупности применяются показатели, которые называют структурнымисредними.
Медиана (Me)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна. - Статистика — Структурныесредниевеличины. Модаимедиана
Модаимедиана. Для характеристики структуры статистической совокупности применяются показатели, которые называют структурнымисредними.
Медиана (Me)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна. - Статистика — Средниевеличины: понятие, виды
2.структурныевеличины Особый вид ср. вел-н структур. средние — применяется для изучения внутр строения рядов распр-я значений признака, а также
Для изучения структуры явления и выявления структур сдвигов прим. стукт. среднейвеличины – это модаимедиана. - Правовая статистика — Понятие среднейвеличины
Понятие среднейвеличины. Средниевеличины также, как и относительные, являются разновидностью обобщающих показателей.
— структурныесредние (модаимедиана); — средняя прогрессивная и другие (например, средняя геометрическая, средняя гармоническая). - Статистика — Виды среднихвеличин
Структурныесредниевеличины. Модаимедиана.
Виды среднихвеличин. Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая. - Правовая статистика — Модаимедиана
Средняя арифметическая является наиболее распространенным видом среднихвеличин.
Относительные величины – это обобщающие показатели, которые хар-ют явления в их соотношении друг с д. Модаимедиана. - Теория статистики — Виды среднихвеличин
Структурныесредниевеличины. Модаимедиана.
Виды среднихвеличин. Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя геометрическая; средняя гармоническая; средняя квадратическая. - Статистика — Понятие вариации
Структурныесредниевеличины. Модаимедиана.
Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе, возникает под влиянием факторов кроме положенного в основу группировки. - Теория статистики — Понятие вариации
Структурныесредниевеличины. Модаимедиана.
Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе, возникает под влиянием факторов кроме положенного в основу группировки. - Шпаргалки по Теории статистики
Виды среднихвеличин. Математическая статистика использует различные средние, такие как: средняя арифметическая; средняя г. подробнее ». Структурныесредниевеличины. Модаимедиана.
 найдено похожих страниц:10
найдено похожих страниц:10
Понятие и виды средних величин
Средняя величина — это обобщающий показатель статистической совокупности, который погашает индивидуальные различия значений статистических величин, позволяя сравнивать разные совокупности между собой.
Существует 2 класса средних величин: степенные и структурные .
К структурным средним относятся мода и медиана, но наиболее часто применяются степенные средние различных видов.
Степенные средние величины
Степенные средние могут быть простыми и взвешенными.
Простая средняя величина рассчитывается при наличии двух и более несгруппированных статистических величин, расположенных в произвольном порядке по следующей общей формуле средней степенной (при различной величине k (m)):
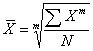
Взвешенная средняя величина рассчитывается по сгруппированным статистическим величинам с использованием следующей общей формулы:
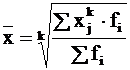
где x — средняя величина исследуемого явления;
xi – i -й вариант усредняемого признака 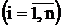 ;
;
fi – вес i -го варианта.
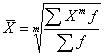
где X – значения отдельных статистических величин или середин группировочных интервалов;
m — показатель степени, от значения которого зависят следующие виды степенных средних величин:
при m = -1 средняя гармоническая;
при m = 0 средняя геометрическая;
при m = 1 средняя арифметическая;
при m = 2 средняя квадратическая;
при m = 3 средняя кубическая.
Используя общие формулы простой и взвешенной средних при разных показателях степени m, получаем частные формулы каждого вида, которые будут далее подробно рассмотрены.
Средняя арифметическая
Средняя арифметическая – начальный момент первого порядка, математическое ожидание значений случайной величины при большом числе испытаний;
Средняя арифметическая — это самая часто используемая средняя величина, которая получается, если подставить в общую формулу m=1. Средняя арифметическая простая имеет следующий вид:
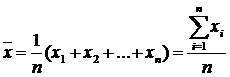 или
или
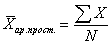
где X — значения величин, для которых необходимо рассчитать среднее значение; N — общее количество значений X (число единиц в изучаемой совокупности).
Средняя арифметическая взвешенная имеет следующий вид:
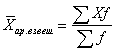
где f — количество величин с одинаковым значением X (частота).
Если значения X заданы в виде интервалов, то для расчетов используют середины интервалов X, которые определяются как полусумма верхней и нижней границ интервала. А если у интервала X отсутствует нижняя или верхняя граница (открытый интервал), то для ее нахождения применяют размах (разность между верхней и нижней границей) соседнего интервала X.
Функция СРЗНАЧ вычисляет среднее (арифметическое) своих аргументов.
Функция СРЗНАЧА вычисляет среднее арифметическое значений, заданных в списке аргументов. Помимо чисел в расчете могут участвовать текст и логические значения, такие как ИСТИНА и ЛОЖЬ.
Средняя гармоническая для определения средней суммы обратных величин;
Средняя гармоническая применяется, когда исходные данные не содержат частот f по отдельным значениям X, а представлены как их произведение Xf. Обозначив Xf=w, выразим f=w/X, и, подставив эти обозначения в формулу средней арифметической взвешенной, получим формулу средней гармонической взвешенной:
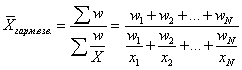
Таким образом, средняя гармоническая взвешенная применяется тогда, когда неизвестны частоты f, а известно w=Xf. В тех случаях, когда все w=1, то есть индивидуальные значения X встречаются по 1 разу, применяется формула средней гармонической простой:
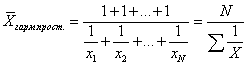
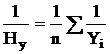
Функция СРГАРМ в озвращает среднее гармоническое множества данных. Среднее гармоническое — это величина, обратная к среднему арифметическому обратных величин.
Среднее гармоническое всегда меньше среднего геометрического, которое всегда меньше среднего арифметического.
Средняя геометрическая
Средняя геометрическая для оценки средних темпов роста случайной величин, нахождения значения признака, равноудаленного от минимального и максимального значения;
Средняя геометрическая применяется при определении средних относительных изменений. Геометрическая средняя величина дает наиболее точный результат осреднения, если задача стоит в нахождении такого значения X, который был бы равноудален как от максимального, так и от минимального значения X.
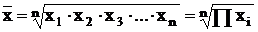
Функция СРГЕОМ в озвращает среднее геометрическое значений массива или интервала положительных чисел.
Средняя квадратическая – начальный момент второго порядка.
Средняя квадратическая применяется в тех случая, когда исходные значения X могут быть как положительными, так и отрицательными, например при расчете средних отклонений.
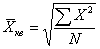
Главной сферой применения квадратической средней является измерение вариации значений X.
Средняя кубическая
Средняя кубическая – начальный момент третьего порядка.
Средняя кубическая применяется крайне редко, например, при расчете индексов нищеты населения для развивающихся стран (ИНН-1) и для развитых (ИНН-2), предложенных и рассчитываемых ООН.
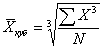
Copyright © 2010-2020
Ющик Е.В. All Rights Reserved
ЛитЛайф
Помогите нам сделать Литлайф лучше
- «
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- .
- 48
- 49
- »
- Перейти
Людмила Михайловна Неганова
Статистика: Конспект лекций
ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
Тема 1. СТАТИСТИКА КАК НАУКА
1.1. Предмет и метод статистики как общественной науки
В самой природе человека заложено стремление к познанию мира, которое находит свое выражение в изучении и развитии особых отраслей знания – наук. Каждая наука, обращая свой взгляд на явления реального мира, вырабатывает специфические особенности, отличающие одну науку от другой. Суть любой науки заключается в объекте и предмете познания, причем разные науки могут иметь один объект познания, но разные предметы.
Объект науки– явления реального мира, на которые наука распространяет свое познание. Предмет науки – определенный круг вопросов относительно объекта исследования, которые относятся к части явления или к некоторым областям объекта. При выяснении предмета науки решается вопрос о том, что изучает данная наука. Принципы и методы изучения предмета науки составляют ее методологию.
Статистика – самостоятельная общественная наука, имеющая свой предмет и методы исследования, которая возникла из потребностей общественной жизни. Термин «статистика» происходит от латинского слова «статус», которое означает «положение, порядок». Впервые его употребил немецкий ученый Г. Ахенваль (1719–1772).
В настоящее время термин «статистика» употребляется в трех значениях:
• особая отрасль практической деятельности людей, направленная на сбор, обработку и анализ данных, характеризующих социально-экономическое развитие страны, ее регионов, отдельных отраслей экономики или предприятий;
• наука, занимающаяся разработкой теоретических положений и методов, используемых в статистической практике;
• статистические данные, представленные в отчетности предприятий, отраслей экономики, а также данные, публикуемые в сборниках, различных справочниках, бюллетенях и т. п.
Объект статистики – это явления и процессы социально-экономической жизни общества, в которых отражаются и находят свое выражение социально-экономические отношения людей. В зависимости от объекта изучения статистика как наука подразделяется на несколько блоков (рис. 1).

Рис. 1.1. Структура статистической науки
Общая теория статистики является методологической основой, ядром всех отраслевых статистик, она разрабатывает общие принципы и методы статистического исследования общественных явлений и является наиболее общей категорией статистики.
Задача экономической статистики – разработка и анализ синтетических показателей, отражающих состояние национальной экономики, взаимосвязи отраслей, особенности размещения производительных сил, наличие материальных, трудовых и финансовых ресурсов. Социальная статистика формирует систему показателей для характеристики образа жизни населения и различных аспектов социальных отношений.
В целом статистика занимается сбором информации различного характера, ее упорядочиванием, сопоставлением, анализом и интерпретацией (объяснением) и обладает следующими отличительными особенностями. Во-первых, статистика изучает количественную сторону общественных явлений: величину, размер, объем и имеет числовое значение. Во-вторых, статистика исследует качественную сторону явлений: специфику, внутреннюю особенность, отличающую одно явление от других. Качественная и количественная стороны явления всегда существуют вместе, образуя единство.
Все общественные явления и события протекают во времени и в пространстве, и в отношении любого из них всегда можно установить, когда оно возникло и где оно развивается. Таким образом, статистика изучает явления в конкретных условиях места и времени.
Изучаемые статистикой явления и процессы общественной жизни находятся в постоянном изменении, развитии. На основе сбора, обработки и анализа массовых данных об изменении изучаемых явлений и процессов выявляется статистическая закономерность. В статистических закономерностях проявляются действия общественных законов, которые определяют существование и развитие социально-экономических отношений в обществе.
Предметом статистики является изучение общественных явлений, динамики и направления их развития. При помощи статистических показателей данная наука определяет количественную сторону общественного явления, наблюдает закономерности перехода количества в качество на примере данного общественного явления и на основании этих наблюдений производит анализ данных, полученных в определенных условиях места и времени. Статистика исследует социально-экономические явления и процессы, которые носят массовый характер, изучает множество определяющих их факторов.
Большинство общественных наук пользуются статистикой для выведения и подтверждения своих теоретических законов. Выводами, основанными на статистических исследованиях, пользуются экономика, история, социология, политология и многие другие гуманитарные науки. Статистика необходима не только общественным наукам для подтверждения их теоретической основы, но велика и практическая ее роль: ни одно крупное предприятие или серьезное производство, разрабатывая стратегию экономического и социального развития объекта, не может обойтись без анализа данных статистического учета. Для этого на предприятиях создаются специальные аналитические отделы и службы, которые привлекают специалистов, прошедших профессиональную подготовку по данной дисциплине.
Как любая наука, статистика имеет определенную методологию изучения своего предмета. Как уже отмечалось выше, ее в основном интересует развитие явления и его связь с другими явлениями общественной жизни, поэтому метод статистики выбирается в зависимости от изучаемого явления и конкретного предмета изучения. В статистике разработаны и применяются специфические способы и приемы исследования общественных явлений, которые в совокупности и образуют метод статистики. К ним относятся наблюдение, сводка и группировка данных, исчисление обобщающих показателей на основе специальных методов (метод средних индексов и т. д.). В соответствии с вышесказанным различают три этапа работы со статистическими данными:
• сбор;
• группировка и сводка;
• обработка и анализ.
Под сбором данных понимают массовое научно-организованное наблюдение, посредством которого получают первичную информацию об отдельных фактах (единицах) исследуемого явления. Такой статистический учет большого числа или всех входящих в состав изучаемого явления единиц является информационной базой для статистических обобщений, для формулирования выводов об изучаемом явлении или процессе. Под группировкой и сводкой данных понимают распределение множества фактов (единиц) на однородные группы и подгруппы, подсчет итогов по каждой группе и подгруппе и оформление полученных итогов в виде статистической таблицы.
Статистический анализ является заключительной стадией статистического исследования. Он включает в себя обработку статистических данных, полученных при сводке, интерпретацию полученных результатов с целью получения объективных выводов о состоянии изучаемого явления и закономерностях его развития. В процессе статистического анализа изучаются структура, динамика и взаимосвязь общественных явлений и процессов.
К основным этапам статистического анализа относят:
• установление фактов и их оценку;
• выявление характерных особенностей и причин явления;
• сопоставление явления с нормативными, плановыми и прочими явлениями, принятыми за базу сравнения;
• формулирование выводов, прогнозов, предположений и гипотез;
Мода. Медиана. Способы их расчета (стр. 1 из 2)
Накопленная частота, впервые превышающая это значение, S = 41, ей соответствует значение признака x = 37 размер. Следовательно, Me = 37 размер обуви, т.е. половина пар покупается меньше 37-го размера, а другая половина – больше.
В этом примере мода и медиана совпадают, но они могут и не совпадать.
В интервальном вариационном ряду определяются накопленные частоты, по данным о накопленных частотах находят медианный интервал – интервал, в котором накопленная частота составляет половину или впервые превышает половину всей суммы частот. Формула для определения медианы в интервальном ряду распределения имеет следующий вид:
 .
.
где xMe – нижняя граница медианного интервала;
iMe – величина медианного интервала;
∑fi – сумма частот ряда;
SMe-1 – сумма накопленных частот интервала, предшествующего медианному;
fMe – частота медианного интервала.
Пример. Определить медиану по имеющимся данным (табл. 7.8).
Таблица 7.8 – Распределение работников по стажу
| Стаж, лет | Число работников, чел. | Накопленные частоты |
| до 2 2-4 4-6 6-8 8-10 свыше 10 | ||
| Итого | х |
По данным табл. 8 определим порядковый номер медианы: NMe=100/2=50. Накопленная частота, впервые превышающая это значение, S = 82, ей соответствует интервал 6-8 лет (медианный интервал). В этом примере модальный и медианный интервал совпадают, но они могут и не совпадать. Определим медиану по формуле:
 лет
лет
Следовательно, Me = 6,2 года, т.е. половина работников имеют стаж менее 6,2 года, а другая половина – более.
Мода и медиана находят широкое применение в разных областях экономики. Так, исчисление модальной производительности труда, модальной себестоимости и т.д. дает возможность экономисту судить о преобладающем в данный момент их уровне. Эта характеристика должна быть использована для выявления резервов нашей экономики. Мода имеет значение для решения практических задач. Так, при планировании массового выпуска одежды и обуви устанавливается размер продукции, который пользуется наибольшим спросом (модальный размер). Мода может быть использована в качестве приближенной характеристики уровня изучаемого признака вместо средней арифметической, если распределения частот близко к симметричному и имеет одну неплоскую вершину.
Медиану следует применять в качестве средней величины в тех случаях, где нет достаточной уверенности в однородности изучаемой совокупности. На медиану влияют не столько сами значения, сколько число случаев на том или ином уровне. Следует также отметить, что медиана всегда конкретна (при большом числе наблюдений или в случае нечетного числа членов совокупности), т.к. под Ме подразумевается некоторый действительный реальный элемент совокупности, тогда как арифметическая средняя часто принимает такое значение, которое не может принимать ни одна из единиц совокупности.
Главное свойство Ме в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины:  . Это свойство Ме может быть использовано, например, при определении места строительства общественных зданий, т.к. Ме определяет точку, дающую наименьшее расстояние, допустим, детских садов от местожительства родителей, жителей населенного пункта от кинотеатра, при проектировке трамвайных, троллейбусных остановок и т.д.
. Это свойство Ме может быть использовано, например, при определении места строительства общественных зданий, т.к. Ме определяет точку, дающую наименьшее расстояние, допустим, детских садов от местожительства родителей, жителей населенного пункта от кинотеатра, при проектировке трамвайных, троллейбусных остановок и т.д.
В системе структурных показателей в качестве показателей особенностей формы распределения выступают варианты, занимающие определенное место в ранжированном вариационном ряду (каждое четвертое, пятое, десятое, двадцать пятое и т.д.). Аналогично с нахождением медианы в вариационных рядах можно отыскать значение признака у любой по порядку единицы ранжированного ряда.
Квартили – значения признака, делящие ранжированную совокупность на четыре равные части. Различают квартиль нижний (Q1), средний (Q2) и верхний (Q3). Нижний квартиль отделяет 1/4 часть совокупности с наименьшими значениями признака, верхний — 1/4 часть с наибольшими значениями признака. Это означает, что 25% единиц совокупности будут меньше по величине Q1; 25% единиц будут заключены между Q1 и Q2; 25% – между Q2 и Q3; остальные 25% превосходят Q3. Средним квартилем (Q2) является медиана.
Для расчета квартилей по интервальному ряду используют формулы:
 ;
;
 .
.
где xQ1 – нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%);
xQ3 – нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%);
SQ1-1 – накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль;
SQ3-1 – накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль;
fQ1– частота интервала, содержащего нижний квартиль;
fQ3 – частота интервала, содержащего верхний квартиль.
Децили – это значения вариант, которые делят ранжированный ряд на десять равных частей: 1-ый дециль (d1) делит совокупность в соотношении 1/10 к 9/10, 2-ой дециль (d2) — в соотношении 2/10 к 8/10 и т.д. Вычисляются децили по той же схеме, что и медиана, и квартили:
 ;
;
 .
.
Использование в анализе вариационных рядов распределения рассмотренных выше характеристик позволяет глубоко и детально охарактеризовать изучаемую совокупность.
Дата добавления: 2015-12-26; просмотров: 510;
По теме: методические разработки, презентации и конспекты

Методическая разработка для выполнения практической работы учебная дисциплина: статистика тема: Относительные и средние величины
Методическая разработка практической работы составлена для студентов, обучающихся по специальности 080114 «Экономика и бухгалтерский учет (по отраслям)» по дисциплине «Статистика», на тему «Относитель.

Методическая разработка для выполнения практической работы учебная дисциплина: экономическая статистика тема: Индексы цен в статистике внешней торговли.
Методическая разработка практической работы составлена для студентов, обучающихся по специальности 080110 «Экономика и бухгалтерский учет (по отраслям)» по дисциплине «Экономическая статистика», на те.

Презентация на тему «Предмет, метод, задачи статистики и принципы организации государственной статистики в РФ»
Эта презентация предназначена для использования на уроке «Предмет, метод, задачи статистики и принципы организации государственной статистики в Р.Ф.».Представленная в презентации информация в наг.

Презентация на тему «Статистика населения»
Эта презентация предназначена для использования на кружке «Статистик» по теме «Современное представление о статистики населения» Представленная в презентации информация в наглядной и до.

ДОКЛАД НА ТЕМУ: «СРЕДНЕЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАНИЕ В СИСТЕМЕ НЕПРЕРЫВНОГО ОБРАЗОВАНИЯ»
Глобальные изменения, происходящие в условиях научно-технического прогресса, экономических и политических сдвигов, привели к необратимым изменениям в образовании, к осознанию его особой социальной рол.
Тема: Средние величины в статистике: средняя арифметическая, средняя квадратическая, средняя гармоническая.

Презентация на тему «Математическая статистика»
Презентация для студентов СПО и НПО по дисциплине «Математика» на тему «Математическая статистика".